Female: Male:
60 35
96 109
26 31
n₁=no. of entries=3 n₂=no. of entries=3
s₁=sample standard s₂=sample standard
deviation=35.005 deviation=43.924
x₁=sample mean=60.666 x₂=sample mean=58.333
Here s and x are calculated from calculator.
Now,
for significance level
1-α=90%
1-α=0.9
α=0.1
α/2=0.05
As population variances are unknown for both Male and female so the best suitable formula is
(x₁ - x₂) ± tα/2,v₁ *
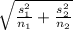
........1
where v(degree of fredom)=(s₁²/n₁+s₂²/n₂)² / ((s₁²/n₁)²/n₁-1)+(s₂²/n₂)²/n₂-1))
by putting values
v=3.81026
From Statistics table,
See the t table at α/2=0.05 and v=3.81026
use interpolation as v value is not in the table,
3.81026-3/4-3 = x-3.182/2.776-3.182
x= 2.853
by putting values in eq. 1 we get
(60.666-58.333) ± (2.853)*
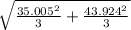 2.333 ± 92.516 is the correct answer.
2.333 ± 92.516 is the correct answer.