The formula we need is this one:

. Filling in accordingly, we have x+4(x+4+1)=x+1(x+1+11). Simplifying that we get (x+4)(x+5)=(x+1)(x+12). We will FOIL both sides to get
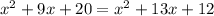
. Combining like terms gives us this simplification: 0=4x-8. If we factor out the common 4, we have 0 = 4(x-2). By the Zero Product Property, eitheer 4=0 or x-2=0. Well obviously, 4 does not equal zero, so x-2 = 0, and x = 2.