Answer:
Option 1 - The composition was done in the incorrect order.
Explanation:
Given :
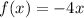 and
and
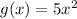 . Andrew finds the composition [f o g](x) as shown below.
. Andrew finds the composition [f o g](x) as shown below.
= 5(-4x)^2 = 5(16x^2) = 80x^2](https://img.qammunity.org/2019/formulas/mathematics/high-school/hvz9vy1xik2861bnm71nvodel2bo88tvym.png)
To find : What error did Andrew make?
Solution :
We have given two functions
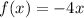 and
and
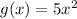
Now, we find [f o g](x) i.e, substitute the value of g in f(x)
=f(g(x))=f(5x^2)](https://img.qammunity.org/2019/formulas/mathematics/high-school/nmypw2yx3vh9we9p5mozuhgnczq5qu5j50.png)
=-4(5x^2)](https://img.qammunity.org/2019/formulas/mathematics/high-school/wu8an4iwcqjh13tjyrdsjk4yssa2089djk.png)
=-20x^2](https://img.qammunity.org/2019/formulas/mathematics/high-school/7ibm3dohivvr9gjq888jv5t2h364zcm1nq.png)
Exact solution is
=-20x^2](https://img.qammunity.org/2019/formulas/mathematics/high-school/7ibm3dohivvr9gjq888jv5t2h364zcm1nq.png) .
.
Andrew mistake is that he finds [g o f](x) i.e, he take the composition in incorrect order.
Therefore, Option 1 is correct.
The composition was done in the incorrect order.