Question

denesh is creating a triangular flower bed using three pieces of wood. The two shorter pieces of wood have lengths of 7 feet and 24 feet. How long , in feet , should the third piece of wood be for denesh to create a right triangle?

Answer 1

This is a problem that uses the Pythagorean Theorem.

`a = \sqrt{ {b}^(2) + {c}^(2) } \\ a = \sqrt{ {7}^(2) + {24}^(2) } \\ a = √(49 + 576) \\ a = √(625) \\ a = 25`
The hypotenuse is 25 feet.

Answer 2

The third piece of wood that for denesh need to create to form a right triangle is:

25 feet.

Explanation:

We are given two shorter legs of a wood of lengths as:

7 feet and 24 feet.

We know that in a right angled triangle with two shorter sides as a and b the longer length or the hypotenuse of the triangle of length c is given by Pythagorean Theorem as:

`c^2=a^2+b^2`

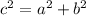
We have:

a=7 and b=24

Hence,

`c^2=7^2+(24)^2\\\\\\c^2=49+576\\\\\\c^2=625\\\\\\c=25`

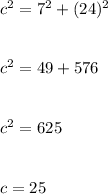
Hence, the length of the third piece of wood should be:

25 feet.