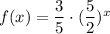Question

Pablo generates the function fx= 3/2(5/2)^x-1 to determine the xth number in a sequence. Which is an equivalent representation?

Answer 1

3/2 = 3 x 1/2
5/2 = 5 x 1/2
so f(x) = 3 x 1/2 x (5 x 1/2) ^ x-1
f(x) = 3 x 1 x (5 x 1/2)^x-1 [notice the 1/2 is together]
-----------------------
2

but x/2 = x/1 divided by 2/1 to divide these, invert and multiply: x/2 x 2/1

so f(x) = 3 x 1 x (5/2 )^x-1
----------------------
2
f(x) = 3 (5/2 ) ^ x-1 (x 1/2)

f(x) = 1.5 (5/2)^x-1

Answer 2

The equivalent function is
`f(x)=(3)/(5)\cdot ((5)/(2))^(x)`

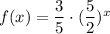
Explanation:

Given: Pablo generates the function
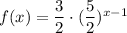`f(x)=(3)/(2)\cdot ((5)/(2))^(x-1)` to determine the xth number in a sequence.

To find : The equivalent representation?

Solution :

`f(x)=(3)/(2)\cdot ((5)/(2))^(x-1)`

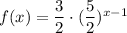
We will re-write the function,

We distribute the exponent x-1

`f(x)=(3)/(2)\cdot ((5)/(2))^(x)\cdot ((5)/(2))^(-1)`

`\because a^(m+n)=a^m\cdot a^n`

`f(x)=(3)/(2)\cdot ((5)/(2))^(x)\cdot (2)/(5)`

`\because ((a)/(b))^(-1)=(b)/(a)`

`f(x)=(3)/(2)\cdot (2)/(5)\cdot ((5)/(2))^(x)`

`f(x)=(3)/(5)\cdot ((5)/(2))^(x)`

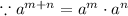
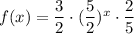
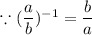
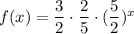
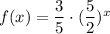
Hence, The equivalent function is

`f(x)=(3)/(5)\cdot ((5)/(2))^(x)`