Question

Match the systems of linear equations with their solutions.

Answer 1

Counting from the left the 7th equations have infinite solutions. (because the first equation = 3 * the second) In effect the same equation.

9th equations from the left . If we multiply the first equation by 3 we get same expression on the left side as the second but in first equation we have 12 on right side and in second theres 11 on right side. This is absurd so No solution.

AS for the other 4 equations plug in the given values in the ordered pairs to find the matches

Answer 2

Explanation:

A). Linear equation are x + y = -1 ----------(1)

and -6x + 2y = 14 ------(2)

First we multiply equation 1 by 6 then we add it to equation 2.

6(x + y) + (-6x + 2y) = -6 + 14

6x + 6y - 6x + 2y = 8

8y = 8

y = 1

By putting y = 1 in the equation 1

1 + x = -1

x = -1 -1 = -2

Solution will be (-2, 1)

B). Linear equations are x - 2y = -5 -----(1)

and 5x + 3y = 27 ------(2)

We multiply equation 1 by 5 and subtract it from 2

(5x + 3y) - 5(x - 2y) = 27 - 5(-5)

5x + 3y - 5x + 10y = 27 + 25

13y = 52

y = 4

By putting y = 4 in equation 1

x = -5 + 2y = -5 + 2(4)

= -5 + 8

= 3

solutions will be (3, 4)

C). -4x + y = -9 -----(1)

5x + 2y = 3 ----(2)

We multiply equation 1 by 2 and subtract it from equation 2

5x + 2y - 2(-4x + y) = 3 - 2(-9)

5x + 2y + 8x - 2y = 3 + 18

13x = 21

x =
`(21)/(13)`

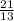
By putting x =
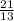`(21)/(13)` in equation 1

y = 9 + 4y

= 9 + 4(
`(21)/(13)`)

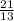= 9 +
`(84)/(13)`

=
`(201)/(13)`

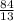
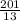
Solution will be
`((21)/(13), (201)/(13))`

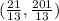
D). 6x + 3y = -6 ---- (1)

2x + y = -2 ------(2)

By multiplying equation 2 by (-3) and add it to equation 1

6x + 3y + (-3)(2x + y) = -6 + (-2)(-3)

6x + 3y - 6x - 3y = -6 + 6

0 = 0

Therefore, this equation has infinite solutions.

E). -x + 2y = 4 ----(1)

-3x + 6y = 11

3(-x + 2y) = 11

-x + 2y =
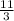`(11)/(3)`-----(2)

So this system of linear equations has no solution.

F). -7x + y = 1 ---- (1)

14x - 7y = 28 -----(2)

We divide equation 2 by 7 and add it to the equation 1

-7x + y + 2x -y = 1 + 4

-5x = 5

x = -1

Now we put x = -1 in equation 1

-7(-1) + y = 1

7 + y = 1

y = 1 - 7

y = -6

So the solution will be (-1, -6)