Question

If a baseball player hits a baseball from 4 feet off the ground with an initial velocity of 64 feet per second, how long will it take the baseball to hit the ground? Use the equation h=-16t^2+64t+4.

Answer 1

Right now that equation is a function of time, h(t), height with respect to time. If the baseball is on the ground, it has no height. In other words, its height = 0. So if we set the equation equal to 0 and solve for t, time, that will tell us the time that the ball had a height of 0. If you plug those numbers into the quadratic formula, which is the best and most efficient way to factor a quadratic, you will get that the times are -.0615528128 and 4.061552813 seconds. The 2 things in math that will never EVER be negative are time and distance/length. So we know that the ball will not hit the ground at -.062 seconds. Therefore, it hits the ground 4.06 seconds after it was hit.

Answer 2

The answer is 4.06 seconds.

Explanation:

1. We need to identify the value of h in the given equation. h stands for the final height of the ball. When the ball hits the ground, the height is 0, hence h=0, and now we replace

`0=-16t^(2) +64t+4`

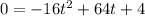
2. We can see this is quadratic equation, hence, we can use the quadratic equation to isolate the time " t". The quadratic formula is:

`(-b+-√(b^2-4ac) )/(2a)\\`

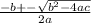
where "a" is the coefficient right next to t^2, "b" is the coefficient right next to t and "c" is the coefficient that is alone. For this problem, we have a=16, b=64 and c=4

3. Now, we can replace

`t=(-64+-√(64^2-4(-16)(4)) )/(2(-16)) \\t=(-64+-65.96 )/(-32) \\`

Using the plus sign (+) we get t=-0.061 sec, and using the less sign (-) we get t=4.06 seconds. We only need to take into account the positive time because there is no sense to have a negative time.