Question

Determine whether the function ƒ(x) = –2x3 – 5x is even, odd, or neither. neither odd even

Answer 1

For this case we have the following function:

`ƒ (x) = -2x ^ 3 - 5x`
By definition, we have to:

A function is even if, for each x in the domain of f, f (- x) = f (x). The even functions have reflective symmetry through the y-axis.

A function is odd if, for each x in the domain of f, f (- x) = - f (x). The odd functions have rotational symmetry of 180º with respect to the origin.

Evaluating f (-x) we have:

`f (-x) = -2 (-x) ^ 3 - 5 (-x)`
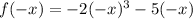
Rewriting:

`f (-x) = - (- 2 (x) ^ 3 - 5 (x)) f (-x) = - f (x)`

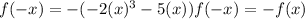
Therefore, according to the definition, the function is odd.

Answer:

`f (-x) = - f (x)`
The function is odd