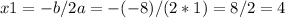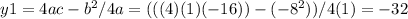Question

The function y=x^2-8x-16 has a___ value of ___
1) maximum or minimum
2) -8,-4,-32,4

Answer 1

minimum value of -32 - u can just plug the equation into a graphing calculator! :)

Answer 2

This function has a minimum value(vertex) =(4,-32)

Explanation:

When you have an quadratic function, you have yo know that there is a General function that describe it:

y=a^2+bx-c

If you have that a>0, then your function has a minimum that is the same than the vertex.

You can calculate the minimum (x1,y1) with this equations:

`x1=-b/2a`

`y1=4ac-b^2/4a`

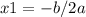
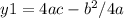
Then you have: y=x^2-8x-16

where:

a=1

b=-8

c=-16

the minimum is:

`x1=-b/2a=-(-8)/(2*1)=8/2=4`

`y1=4ac-b^2/4a=(((4)(1)(-16))-(-8^2))/4(1)=-32`