Question

HELP ASAP What is the length of bc ? Round to the nearest tenth.

6.8 cm

7.5 cm

14.5 cm

17.7 cm

Answer 1

sin(65) = Opp./Hypo. = x/16
x = sin(65) * 16
x = 14.5

Answer
14.5 cm

Answer 2

Answer: The correct option is (C) 14.5 cm.

Step-by-step explanation: We are given to find the length of the side BC in the triangle ABC shown in the figure.

From the figure, we see that

triangle ABC is a right-angled triangle, where

`m\angle C=90^\circ,~~m\angle M=65^\circ,~~AB=16~\textup{cm},~~BC=x=?.`

With respect to angle A, side BC is the perpendicular and AB is the hypotenuse.

So, from trigonometric ratios, we have

`\sin m\angle A=(BC)/(AB)\\\\\\\Rightarrow \sin65^\circ=(x)/(16)\\\\\\\Rightarrow 0.9063=(x)/(16)\\\\\\\Rightarrow x=16* 0.9063\\\\\Rightarrow x=14.5008.`

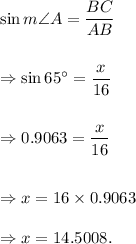
Rounding to the nearest tenth, we get

x = 14.5 cm.

Thus, the length of the side BC is 14.5 cm.

Option (C) is CORRECT.