Answer:
The expression sinx(cscx-cotx cosx) can be simplified to sin²x.
Explanation:
Consider the provided trigonometric expression.
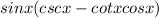
Open the parentheses and apply the distributive property: a(b+c)=ab+ac
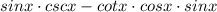
Now use the identity:
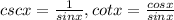
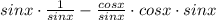
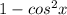
Use the identity: 1 - cos²x = sin²x
Thus,
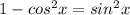
Hence the expression sinx(cscx-cotx cosx) can be simplified to sin²x.