Question

PLEASEE HELP ME 60 POINTS!!!

Match each system of linear equations with the correct number of solutions.

A. No Solution B. Infinitely many solutions C. One Solution

1. y = -4x-5 ------------> _________
y = -4x+1

2. -3x+y = 7 -----------> _________
2x-4y = -8

3. 3x-y = 4 ------------> _________
6x-2y = 8

Answer 1

1. no

2.Inf

3. one

Explanation:

because

Answer 2

1. No Solution

2. One solution

3. Infinitely many solutions

Explanation:

Let us try to solve each of the system of equations one by one.

1.
`y =-4x - 5`

`y = -4x + 1`

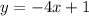
This gives

`-4x- 5 = -4x + 1`

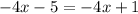
which has no solutions.

2.
`-3x+y=7`

`2x-4y=-8`

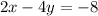
let us write them in y-intercept form

`y=3x+7`

`y=(1)/(2)x+2`

and equate them

`y=3x+7=(1)/(2)x+2`

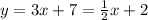
this gives
`x=-2` and

`y=-3(-2)+7 = 1`

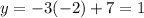
This equation has solutions.

3.
`3x-y=4`

`6x-2y =8`

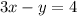
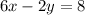
Notice that the second equation is just the first equation multiplied by 2, or

`2(3x-y=4)\rightarrow (6x-2y=8)`

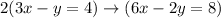
so these are identical equations and therefore this system has infinitely many solutions.

Thus we have

1. No Solution

2. One solution

3. Infinitely many solutions