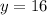As the variables vary inversely, we have the following relationship:
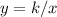
From here, we must find the value of the constant k.
For this, we use the following data:
x = 10 when y = 8
Substituting values we have:
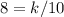
From here, we clear the value of k:
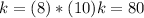
Substituting the value of k we have that the function is:
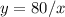
Then, for x = 5 we have:
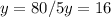 Answer:
Answer:
The function that models the inverse variation is:
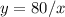 when x = 5:
when x = 5: