Question

If a polynomial function f(x) has roots -9 and 7-i, what must be a factor of f(x)?

Answer 1

By the conjugate root theorem if we have 7-i as a root we have to have 7+i as a root also. Written in factor form, they are (x-(7-i)) and (x-(7+i)). You could rewrite and remove the inner set of parenthesis, but the second of those is what you need. It's choice one above.

Answer 2

`(x-(7+i))` is the answer

Explanation:

a polynomial function f(x) has roots -9 and 7-i

Polynomial roots always come with conjugate pairs

7-i is one of the root

7+i is the another root

So we have three roots

If 'a' is a root then (x-a) is a factor

-9 is one of the root , factor is (x+9)

7-i is a root then factor is
`(x-(7-i))`

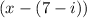
7+i is a root then factor is
`(x-(7+i))`

`(x-(7+i))` is the answer