Question

Use the method of completing the square to transform the quadratic equation into the equation form (x – p)2 = q.

12 - 8x2 + x4 = 0

Answer 1

First things first. We have to get that into standard form.
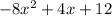
`-8x^2+4x+12` is what I'm seeing. Hope I did not misinterpret. In order to complete the square, we need to do 2 things. First let's set the quadratic equal to 0, then move over the 12 by subtraction.
`-8x^2+4x=-12`. The rule for completing the square is that the leading coefficient HAS to be a +1. Ours is a -8, so we have to factor it out. When we do that, we will get
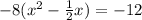
`-8(x^2- (1)/(2)x)=-12`. Now we are ready to complete the square. Take half the linear term, square it, and add it to both sides. Our linear term is 1/2. 1/2 divided by 2 is 1/4. If we square 1/4 we get 1/16. So we add it in. HOWEVER, we have that -8 hanging around out front on the left, refusing to be ignored. If we add in 1/16 into the parenthesis, we have to multiply it by -8 and add whatever that product is onto the right side. -8*1/16= -1/2. This is what all that looks like:
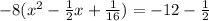
`-8(x^2- (1)/(2)x+ (1)/(16))=-12- (1)/(2)`. In this process we have created a perfect square binomial on the left, which is this:
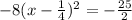
`-8(x- (1)/(4))^2=- (25)/(2)`. If I'm not mistaken, that's the form you need it in.