Question

A train leaves Little​ Rock, Arkansas, and travels north at 85

kilometers per hour. Another train leaves at the same time and travels south at 70

kilometers per hour. How long will it take before they are 465

kilometers​ apart?

Answer 1

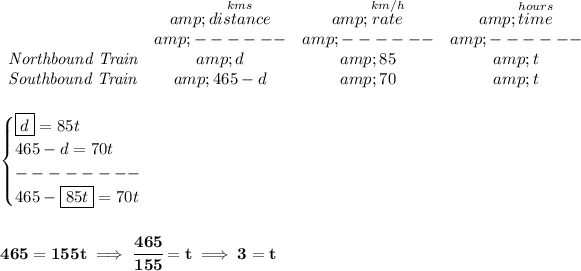
recall your d = rt, distance = rate * time.

we know the train traveling north is going at 85 km/h, and the one traveling south is going 70 km/h.

as they move apart, the distance between them is increased, and at some point is 465 kilometers.

let's say the one traveling north by the time the 465 kilometers are met, has been traveled "d" kilometers, then the one going south has traveled the slack from 465 and "d", namely "465 - d".

let's also keep in mind that since both trains took off at the same time, they have been traveling the same amount of hours, namely "t" hours.


`\bf \begin{array}{lcccl} &\stackrel{km s}{distance}&\stackrel{km/h}{rate}&\stackrel{hours}{time}\\ &------&------&------\\ \textit{Northbound Train}&d&85&t\\ \textit{Southbound Train}&465-d&70&t \end{array} \\\\\\ \begin{cases} \boxed{d}=85t\\ 465-d=70t\\ --------\\ 465-\boxed{85t}=70t \end{cases} \\\\\\ 465=155t\implies \cfrac{465}{155}=t\implies 3=t`