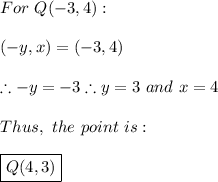We are said that a rectangle has been transformed into the one indicated in Figure 1 according to this rule:
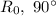
We know that the center of rotation is origin and two rules are applied to rotate a point 90 degrees, namely:
1. Clockwise
In this case, the rule to transform a point is:
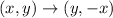
This rule was already applied to form the image, so all we need to do is to reverse the answer using this formula, therefore:
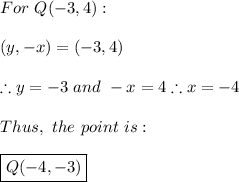
2. Counterclockwise
Applying the same previous concept but with the new rules for this case:
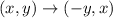
By reversing the answer, we have: