Answer:
center (5,-3), radius = 4
Explanation:
write the center and radius of the circle with equation
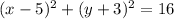
Standard form of the circle is
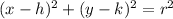
Where (h,k) is the center and r is the radius of the circle
now compare the given equation with standard form
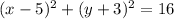
The value of h= 5 and k= -3 and r^2= 16
center (h,k) is (5,-3)
the value of

Take square root on both sides
radius = 4