Question

1. Convert each rate using dimensional analysis. Round to the nearest tenth, if necessary.

9 c /min = ____ qt / h
a.
101.3
c.
120
b.
135
d.
90

2. Convert each rate using dimensional analysis. Round to the nearest tenth, if necessary.

32 cm / s = ____ m / min
a.
0.3
c.
53.3
b.
192
d.
19.2

3. Convert each rate using dimensional analysis. Round to the nearest tenth, if necessary.

25 cm / s = ____ m / h
a.
225
c.
9000
b.
900
d.
90

Answer 1

Using dimensional analysis requires that we set up our ratios so that labels we want to convert cross cancel. In the first one we want cups to be converted to qt, so we have to use the fact that there are 4 c in 1 qt. Then we want to convert minutes to hours so we have to use the fact that there are 60 min in 1 hr. Setting up that conversion looks like this:
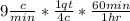
`9 (c)/(min) * (1qt)/(4c)* (60min)/(1hr)`. You cross cancel cups and minutes leaving you with qt on top and hr on the bottom. Doing the math gives you 135 qt/hr. The second one above is set up the same way, but we need the fact now that there are 100 cm in 1 meter, and that there are 60 sec in 1 minute. That looks like this then:
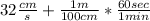
`32 (cm)/(s)+ (1m)/(100cm)* (60sec)/(1min)`. The cm and the seconds cancel leaving meters on top and minutes on bottom. Doing the math on that one gives you 19.2 m/min. The third one is done the same way as the second one, except this time we are using the fact that there are 3600 seconds in 1 hour.
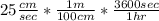
`25 (cm)/(sec) * (1m)/(100cm) * (3600sec)/(1hr)`. The cm and the seconds cancel leaving us with an answer of 900 m/hr