Question

Luis purchases a collectible model car from a dealer. The dealer advises him that the car’s value (The car value is $75 now) will grow by about 9% each year. What is the estimated value of the model car after 10 years?

Answer 1

Judging by the question I generated the equation y=75(1.09^x)
x is the amount of years.
So the equation you should get for 10 years is y=75(1.09^10)
The answer you get should get is $177.55

Answer 2

Answer: $178

Explanation:

We know that the exponential growth equation with rate of growth r in time period x is given by :-

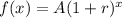`f(x)=A(1+r)^x`, A is the initial value .

Given: The initial value of car = $75

Rate of growth : 9%=0.09

Now, the function represents the car's value after x years is given by ;-

`f(x)=75(1+0.09)^x=75(1.09)^x`

Thus, the value of the model car after 10 years is given by :-

`f(10)=75(1.09)^(10)=177.552275594\approx178` [To the nearest dollar]

Hence, the estimated value of the model car after 10 years = $178