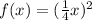Question

If you horizontally stretch the quadratic function, f(x)=x2, by factor of 4, what is the equation of the new function?

Answer 1

For this case, the parent function is given by:

`f (x) = x ^ 2`
We apply the following transformation:
Expansions and horizontal compressions:
The graph of y = f (bx):
If 0 <b <1, the graph of y = f (x) expands horizontally by the factor of 1 / b. (It lengthens)
Applying the transformation we have:

`f (x) = ( (1)/(4) x) ^ 2`
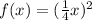
Therefore, the stretch factor is 4, due to:

`(1)/(b) = (1)/((1)/(4) )`
Rewriting:

`(1)/(b) = 4`
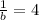Answer:
the equation of the new function is:

`f (x) = ( (1)/(4) x) ^ 2`