Question

A) given the function f(x) = −x 2 + 8x + 9, state whether the vertex represents a maximum or minimum point for the function. explain your answer.

b.rewrite f(x) in vertex form by completing the square.

Answer 1

Since this is a negative parabola, the curve will open downwards like a mountain. A mountain has a peak or a top, aka a maximum. Now let's complete the square to see what that vertex is. Rule is that the leading coefficient has to be a +1. Ours is a -1. So we need to factor it out. First though, set the equation equal to 0 then move the constant away from the x terms to the other side of the equals sign.
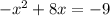
`-x^2+8x=-9`. Factoring out the -1,
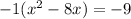
`-1(x^2-8x)=-9`. Now we are ready to complete the square. Take half the linear term, square it, and add it in to both sides. Our linear term is 8. Half of 8 is 4, and 4 squared is 16. So we will add 16 into the set of parenthesis, but don't forget that -1 hanging out front there, refusing to be ignored. It is a multiplier. Therefore, what we have REALLY added in was (-1)(16) = -16. That's what gets added onto the right side to keep things in balance.
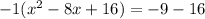
`-1(x^2-8x+16)=-9-16`. We simplify on the right to get -25. Now on the left we will write the perfect square binomial we created while doing this process:
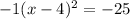
`-1(x-4)^2=-25`. Move the -25 over to the other side by addition and set it back equal to y:
`-1(x-4)^2+25=y`. We see now that our vertex is (4, 25) and that it is a maximum