Question

Find the sum of the first one hundred positive integers. see fig 6.26

Answer 1

Here's a pattern to consider:
1+100=101
2+99=101
3+98=101
4+97=101
5+96=101
.....
This question relates to the discovery of Gauss, a mathematician. He found out that if you split 100 from 1-50 and 51-100, you could add them from each end to get a sum of 101. As there are 50 sets of addition, then the total is 50×101=5050
So, the sum of the first 100 positive integers is 5050.

Quick note
We can use a formula to find out the sum of an arithmetic series:

`s = (n(n + 1))/(2)`
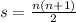
Where s is the sum of the series and n is the number of terms in the series. It works for the above problem.