Question

Simplify the complex fraction. y-1/y^2+y-6/y-6/y+3

A) (y-1)(y-2)/(y-6)(y+2)
B) y-1/(y-6)(y-2)
C) (y-1)(y-6)/(y+3)^2 (y-2)
D) (y-1)(y-6)/(y+3)(y-2)
I really need help on this

Answer 1

Explanation:

try to do a or b

Answer 2

For this case we have the following complex fraction:

`((y-1)/(y^2+y-6) )/((y-6)/(y+3))`
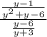
Using the double C method, we can rewrite the given fraction.
We have then:

`((y-1)(y+3))/((y^2+y-6)(y-6))`
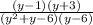
Then, we must factor the quadratic expression into the denominator.
We have then:

`((y-1)(y+3))/((y-2)(y+3)(y-6))`
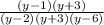
Finally, we cancel similar terms.
We have then:

`((y-1))/((y-2)(y-6))`
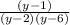Answer:
the complex fraction simplified is:
B) y-1/(y-6)(y-2)