Question

Which explanation provides the best real-world scenario of the graph? If an object is dropped from a height of 38 feet, the function h(t) = –16t2 + 38 gives the height of the object after t seconds. If an object is dropped from a height of –16 feet, the function h(t) = –16t2 + 38 gives the height of the object after t seconds. If an object is dropped from a height of 38 feet, the function h(t) = –16t2 – 38 gives the height of the object after t seconds.

Answer 1

Answer: If an object is dropped from a height of 38 feet, the function h (t) = -16t2 + 38 gives the height of the object after seconds

Explanation:

Answer 2

The equation that models the movement of the object is:

`h (t) = (1/2) * (a) * (t ^ 2) + v0 * t + h0`
Where,
t: time
a: acceleration due to gravity
v0: initial speed
h0: initial height
Suppose that the object falls with zero initial velocity and from a height of 38 feet.
The equation that models the problem is:

`h (t) = -16t ^ 2 + 38`
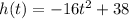Answer:
If an object is dropped from a height of 38 feet, the function h (t) = -16t2 + 38 gives the height of the object after seconds