Question

Solve 2x^2 + 12x = 10. A) -3 +- square root of 14 B) -3 +- 2 of square root of 2 C) -3 +- square root of 19 D) -3 +- square root of 29

Answer 1

We will start solving by moving the 10 over by subtraction and set the polynomial equal to 0 so we can factor.
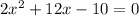
`2x^2+12x-10=0`. I am going to factor out the common 2 to make the numbers a bit smaller for when i put them into the quadratic formula.
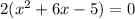
`2(x^2+6x-5)=0` with a=1, b=6, c=-5. Put that into the quadratic formula to get
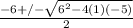
`(-6+/- √(6^2-4(1)(-5)) )/(2)` and
`(-6+/- √(36+20) )/(2)` which simplifies even further to
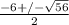
`(-6+/- √(56) )/(2)`. If we simplify that radical it will simplify to
`√(4*14)`. We can pull the perfect square of 4 out as a 2, leaving us with
`2 √(14)`. So altogether we have
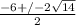
`(-6+/-2 √(14) )/(2)`. The 2 in the denominator will reduce with the other integers (not the radicand!) to give us this as our final answer:
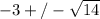
`-3+/- √(14)`, choice A from above.