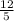Question

11.

Use ∆ABC to find the value of cos B.
21.
Use ∆ABC to find the value of tan B.

(Shorter one is number 11)

Answer 1

cos B =
`(5)/(13)`

tan B =
`(40)/(9)`

Explanation:

• cos Θ = adjacent / hypotenuse
• sin Θ = opposite / hypotenuse
• tan Θ = opposite / adjacent

11) cos B

• the adjacent leg is 15
• the hypotenuse is 39

since cos Θ = adjacent / hypotenuse

then cos B =
`(15)/(39)`

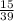
dividing both the numerator and denominator by 3 in order to simplify the answer

cos B =
`(5)/(13)`

For the other picture

• the adjacent leg is 9
• the hypotenuse is 41

since cos Θ = adjacent / hypotenuse

then cos B =
`(9)/(41)`

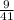
21) tan B

• the opposite leg is 40
• the adjacent leg is 9

since tan Θ = opposite / adjacent

then tan B =
`(40)/(9)`

For the other picture

• the opposite leg is 36
• the adjacent leg is 15

since tan Θ = opposite / adjacent

then tan B =
`(36)/(15)`

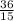
simplifying (diving numerator and denominator by 3)

tan B =
`(12)/(5)`

Answer 2

The first thing we are going to do for this case is to define the cosine and the tangent:
For the cosine we have:

`Cos (x) = (C.A)/(h)`
Where,
C.A: adjacent leg
h: hypotenuse
On the other hand we have that the tangent is given by:
Where,

`Tan (x) = (C.O)/(C.A)`
Where,
C.O: opposite leg
C.A: adjacent leg
We have then:

Part A

`Cos (B) = (15)/(39)`
Simplifying:

`Cos (B) = (5)/(13)`

Part B

`Tan (B) = (40)/(9)`