hello!

since we have the x-intercept of the line, we can just write it as a point:
(-5, 0)
x-intercepts always have a y-coordinate of 0.
now, let's do the same thing with the y-intercept; only note that y-intercepts always have an x-coordinate of 0.
hence, the points are
(-5, 0) and (0, -3)
let's use the points to find the slope:
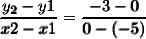
simplify:
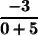
simplify:
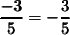
that's the slope; now, we know the y-intercept, so just plug in the values:
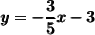

note:-
Hope everything is clear; if you need any more explanation, kindly let me know.