Question

What is the midpoint of the x-intercepts of f(x) = (x – 4)(x + 4)?

(0,0)
(0,4)
(–4,0)
(2,0)

Answer 1

f(x) = (x – 4)(x + 4) = x^2 - 4. This is the equation of a parabola with vertex at (0,-4) and x-intercepts of (-2,0) and (2,0). The midpoint of the line segment connecting these 2 points is (0,0). Draw this situation and see for yourself!

Answer 2

Answer: The correct option is (A) (0, 0).

Step-by-step explanation: We are given to find the midpoint of the x-intercepts of the following quadratic function:

`f(x)=(x-4)(x+4)~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We know that the x-intercepts of a function f(x) is found by solving the equation f(x) = 0.

So, from equation (i), we have

`f(x)=0\\\\\Rightarrow (x-4)(x+4)=0\\\\\Rightarrow x-4=0,~~~~~x+4=0\\\\\Rightarrow x=4,~-4.`

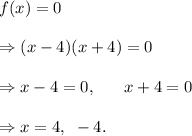
That is, the x-intercepts of the given function are the points (4, 0) and (-4, 0).

Therefore, the co-ordinates of the mid-point of the x-intercepts (4, 0) and (-4, 0) will be

`\left((4+(-4))/(2),(0+0)/(2)\right)\\\\\\=(0,0).`

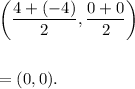
Thus, the required mid-point of the x-intercepts is (0, 0).

Option (A) is correct.