Answer:
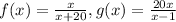
Explanation:
we know that
To find the inverse of a function, exchange variables x for y and y for x. Then clear the y-variable to get the inverse function.
we will proceed to verify each case to determine the solution of the problem
case A)

Find the inverse of f(x)
Let
y=f(x)
Exchange variables x for y and y for x
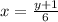
Isolate the variable y
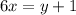
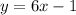
Let
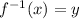
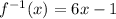
therefore
f(x) and g(x) are inverse functions
case B)
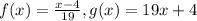
Find the inverse of f(x)
Let
y=f(x)
Exchange variables x for y and y for x
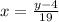
Isolate the variable y

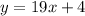
Let
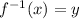
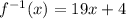
therefore
f(x) and g(x) are inverse functions
case C)
![f(x)=x^(5), g(x)=\sqrt[5]{x}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/zte357quyqonkibmnqf0wpbn47t5yjgdoc.png)
Find the inverse of f(x)
Let
y=f(x)
Exchange variables x for y and y for x
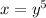
Isolate the variable y
fifth root both members
![y=\sqrt[5]{x}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/zygiztcghybprs99dqif3jxurmt5i5y6w5.png)
Let
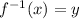
![f^(-1)(x)=\sqrt[5]{x}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/lwnpqni2ybifknf20zz9nj5i06y6nxnnlf.png)
therefore
f(x) and g(x) are inverse functions
case D)
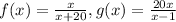
Find the inverse of f(x)
Let
y=f(x)
Exchange variables x for y and y for x
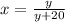
Isolate the variable y
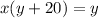
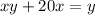
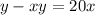
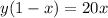
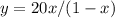
Let
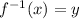
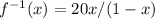
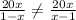
therefore
f(x) and g(x) is not a pair of inverse functions