Question

Sketch the following to help answer the question. Kite WXYZ has a short diagonal of XZ and a long diagonal of WY. The diagonals intersect at point V. The length of XZ = 10cm, and the ∠XYV = 30°. Find the length of segment VY.

20cm
10√3cm
10cm
5√3cm

Answer 1

5√3cm

Explanation:

Sketch the following to help answer the question. Kite WXYZ has a short diagonal of XZ and a long diagonal of WY. The diagonals intersect at point V. The length of XZ = 10cm, and the ∠XYV = 30°. Find the length of segment VY.

20cm

10√3cm

10cm

5√3cm

Odyssey

The person above me is correct

Answer 2

Where the diagonals intersect several things occur. 4 right angles result from this, and they bisect each other. If XZ is 10, then XV is 5. The angle XYV then will be used as the reference angle (30), the side across from it is XV=5, and the side adjacent VY, is the one we are looking for. We will use the tangent ratio, since that is the one that relates the reference angle to the side opposite and the side adjacent. Therefore,
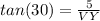
`tan(30)= (5)/(VY)` and
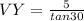
`VY= (5)/(tan30)`. That means that segment VY = 8.66, which, if you're using your Pythagorean triples, is equal to
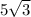
`5 √(3)`. The side across from the 30 angle is x, the side across from the 60 angle is
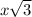
`x √(3)`. We know that the side across from the 30 angle is 5, therefore the side across from the 60 angle is
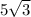
`5 √(3)`. If you put that into your calculator, you'll get the value that I gave you in decimal. Same thing, just a different way of expressing it.