The
correct answer is:
The relationship is linear, and the equation is
y-5 = 2(x+7).
Step-by-step explanation:
To determine if the relationship is linear, we find the slope between each pair of points. Slope is given by the formula:

The slope between the
first two points is given by:
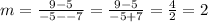
The slope between the
second pair of points is given by:
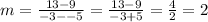
The slope between the
third pair of points is given by:
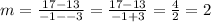
Since the
slope is the same throughout the data, the
relationship is linear and the slope is 2.
To write the equation, we use point-slope form, which is:
y-y₁ = m(x-x₁)
Using the first point, we have:
y-5 = 2(x--7)
y-5 = 2(x+7)