Replace f(x) and g(x) with what they equal:

The formula for subtracting equations is given out by the following expression:
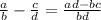
Plug the values in the equation in this formula:
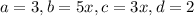
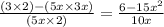
You can transfer positives and negatives from the numerator to the denominator by multiplying each term by -1, as they will equal the same:
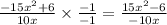
The answer is
D.