Question

A Ferris wheel at an amusement park is modeled by (x – 70)2 + (y – 77)2 = 5,184, where the measurements are in feet. A slingshot attraction is modeled by y = –4x2 + 40x + 50. Which attraction reaches a greater height, and what does it represent in terms of the context?

A. The slingshot reaches a greater height at 50 feet, which is the vertex of the parabola.
B. The Ferris wheel reaches a greater height at 184 feet, which is the highest point on the circle.
C. The Ferris wheel reaches a greater height at 149 feet, which is the highest point on the circle.
D. The slingshot reaches a greater height at 150 feet, which is the vertex of the parabola.

Answer 1

D. The slingshot reaches a greater height at 150 feet, which is the vertex of the parabola.

Explanation:

First let's examine the given equations

`\displaystyle \rm\\(x -70)^2 + (y-77)^2 = 5184 ............. (1)\\y = -4x^2 + 40x + 50 ............... (2)`

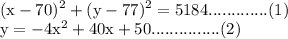
Equation (1) is of the form of a standard equation for a circle

`\displaystyle \rm (x-a)^2 + y-b)^2 = r^2\\\\`

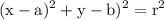
where (a, b) is the center of the circle and r is the radius

Equation (2) is the standard equation of a parabola
y = ax² + bx + c where a, b and c are constant

So we know that the Ferris wheel motion is circular while the slingshot motion is parabolic

Let's compute the highest point at which the Ferris wheel reaches.

Given,

`\displaystyle (x-70)^2 + (y-77)^2 = 5184`
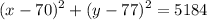
We can see that r² = 5182 by comparing it to the circle equation
`\displaystyle x_v=-(40)/(2\left(-4\right))`

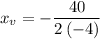
Therefore r = √5184 = 72. The diameter = 144 which is the highest point vertically from the center of the circle

The highest point on the circle = 144 + 5= 149 m since there is a 5' gap between the Ferris wheel and the ground at the lowest point so that has to be taken into account

For the parabola the vertex is the highest point and its x-coordinate given by
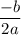`\displaystyle (-b)/(2a)` in the standard equation for a parabola

Comparing the given equation with the standard equation we see that a = -4, b = 40 and c= 50

Therefore
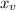`x_v` the x-coordinate of the vertex:

`\displaystyle x_v=-(40)/(2\left(-4\right)) = 5`

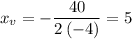
The y coordinate of the vertex can be found by plugging in this value into the parabolic equation

`\displaystyle y_v=-4\cdot \:5^2+40\cdot \:5+50 = 150`

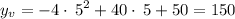
This being the vertical coordinate of vertex of the parabola, the highest point that the slingshot reaches is 150'

So correct answer is D