Answer:
The correct option is A.
Explanation:
The given expression is
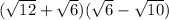
Using distributive property of multiplication, we get
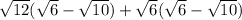
Using distributive property of multiplication, we get
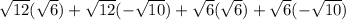
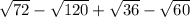
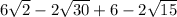
The simplified form of the given expression is
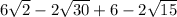 . Therefore the correct option is A.
. Therefore the correct option is A.