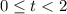Answer:
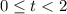
Explanation:
A small rock falling from the top of a 124-ft-tall building with an initial downward velocity of -30 ft/sec is modeled by the equation .
Equation :
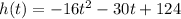
Now we are supposed to find For which interval of time does the rock remain in the air
Substitute h(t)=0

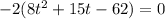
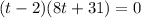
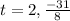
Since time cannot be negative .So, neglect
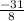
So, time interval for which the rock remain in the air: