Question

Which of these is the area of a sector of a circle with r = 18”, given that its arc length is 6π?

a.54.00 in2B)113.10 in2C)169.65 in2D)339.29 in2

Answer 1

The formulas for arc length and area of a sector are quite close in their appearance. The formula for arc length, however, is related to the circumference of a circle while the area of a sector is related to, well, the area! The arc length formula is
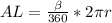
`AL= ( \beta )/(360) *2 \pi r`. Notice the "2*pi*r" which is the circumference formula. The area of a sector is
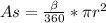
`A s= ( \beta )/(360) * \pi r ^(2)`. Notice the "pi*r squared", which of course is the area of a circle. In our problem we are given the arc length and the radius. What we do not have that we need to then find the area of a sector of the circle is the measure of the central angle, beta. Filling in accordingly,
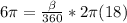
`6 \pi = ( \beta )/(360) *2 \pi (18)`. Simplifying by multiplying by 360 on both sides and then dividing by 36 on both sides gives us that our angle has a measure of 60°. Now we can use that to find the area of a sector of that same circle. Again, filling accordingly,
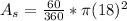
`A_(s) = (60)/(360) * \pi (18) ^(2)`, and
`A_(s) =54 \pi`. When you multiply in the value of pi, you get that your area is 169.65 in squared.