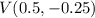We have the following function that is a
quadratic function: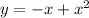
So the graph of this function is shown in the figure below. This is a
parabola as you can see. The roots of this functions, that is, the x-intercepts are:
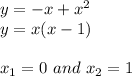
As you can see in the figure. This function decreases from
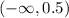
and increases from
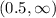
Finally, another thing we can see from the graph is that the vertex is the point: