Answer:
arc XY = 32°
Explanation:
To find : measure of arc XY
∠Z = 39°
Solution :
We will use outside angles theorem
The Outside Angles Theorem: The measure of an angle formed by two secants, two tangents, or a secant and a tangent from a point outside the circle is half the difference of the measures of the intercepted arcs.
In the given figure the intercepted arcs are arc VW and arc XY
Major arc = arc VW = 110°
Minor arc = arc XY
Using theorem ,
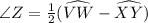
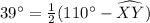
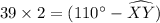
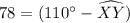
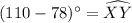
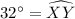
Hence the measure of arc XY = 32°