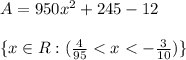Question

In the figure, side AB is given by the expression 5x+5x+3, and side BC is 3x+92x−4. The simplified expression for the area of rectangle ABCD is ________ and the restriction on x is_____

Answer 1

Area = side AB * side BC = (5x + 5x + 3)(3x + 92x - 4)

= (10x + 3)(95x - 4) = 950x^2 - 40x + 285x - 12

= 950x^2 + 245x - 12 Answer

This cannot be negative so restriction on x is 950x^2 + 245x > 12
That is x > 0.0421

Answer 2

`A=950x^2+245-12\\\\\{x\in R: ((4)/(95) <x<-(3)/(10) )\}`

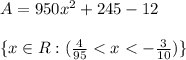
Explanation:

The area of a rectangle is given by:

`A=w*h`

`Where:\\\\w=width\\h=height`

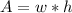
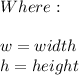
Let:

`h=\overline{\rm AB}=5x+5x+3=10x+3\\\\and\\\\w=\overline{\rm BC}=3x+92x-4=95x-4`

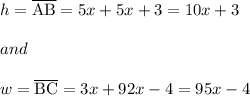
So, the area is given by:

`A=(10x+3)*(95x-4)=950x^2-40x+285x-12=950x^2+245x-12`

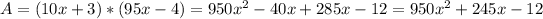
It wouldn't make sense if the result leads us to an area equal to 0 or to a negative area, therefore:

`A=950x^2+245x-12>0`

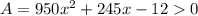
Solving for x using the quadratic formula:

`x=(-b\pm √(b^2-4ac) )/(2a) =(-245\pm √(245^2-4(950)(-12)) )/(2(950)) =(-245\pm √(60025+45600) )/(1900)\\\\x=(-245\pm √(105625) )/(1900)=(-245\pm 325)/(1900)\\\\Hence\\\\x>(4)/(95) \\\\and\\\\x<(-3)/(10)`

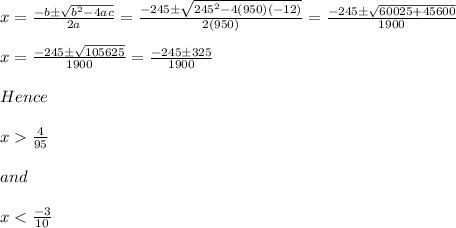
Therefore, the area is given by:

`A=950x^2+245-12\\\\\{x\in R: ((4)/(95) <x<-(3)/(10) )\}`