Answer:
![3\sqrt[3]{3}](https://img.qammunity.org/2019/formulas/mathematics/college/vbsvfco6yw1ca8flw00f41sk126pvbqtcg.png) ; 3 will remain under radical.
; 3 will remain under radical.
Explanation:
We have been given a number
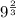 . We are asked to write our given number in simplest radical form.
. We are asked to write our given number in simplest radical form.
Using exponent property for radicals
![a^{(m)/(n)}=\sqrt[n]{x^m}](https://img.qammunity.org/2019/formulas/mathematics/college/y5qibx5pzgq0ol1en8behd3y62e3lvp8i0.png) , we can rewrite our expression as:
, we can rewrite our expression as:
![9^{(2)/(3)}=\sqrt[3]{9^2}](https://img.qammunity.org/2019/formulas/mathematics/college/mknusqqjxomyd4b92xl7dt15t96kypwya5.png)
![9^{(2)/(3)}=\sqrt[3]{81}](https://img.qammunity.org/2019/formulas/mathematics/college/ktw2pdjjx9k3njkc10q9e2n1tqhreuugah.png)
![9^{(2)/(3)}=\sqrt[3]{27*3}](https://img.qammunity.org/2019/formulas/mathematics/college/j7ia2ndmlsyyzrcckhp54vkgeewiy4e4vn.png)
![9^{(2)/(3)}=\sqrt[3]{3^3*3}](https://img.qammunity.org/2019/formulas/mathematics/college/syvkjh9950ymmrgvdyby7vi4repvtle3di.png)
Pulling out 3 from radical, we will get:
![9^{(2)/(3)}=3\sqrt[3]{3}](https://img.qammunity.org/2019/formulas/mathematics/college/ekvbvyl4jl6h7rxne88cdvztnusiq2zg1r.png)
Therefore, the simplest form of our given expression would be
![3\sqrt[3]{3}](https://img.qammunity.org/2019/formulas/mathematics/college/vbsvfco6yw1ca8flw00f41sk126pvbqtcg.png) and 3 will remain under radical.
and 3 will remain under radical.