Question

Which sequence of transformations could be used to map quadrilateral RSTU onto R”S”T”U”?

Answer 1

The correct answer is:


`T_((3,1)) \circ R_(O,270^(\circ))`

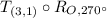Step-by-step explanation:

The coordinates of RSTU are:
R(-5, -4)
S(-4, -2)
T(-1, -3)
U(-3, -5)

The coordinates of R''S''T''U'' are:
R''(-3, 2)
S''(-1, 1)
T''(-2, -2)
U''(-4, 0)


`T_((3, 1))` is a translation 3 units right and 1 unit up. This adds 3 to the x-coordinate of each point and 1 to the y-coordinate of each point. This gives us:
R(-5, -4)→R'(-2, -3)
S(-4, -2)→S'(-1, -1)
T(-1, -3)→T'(2, -2)
U(-3, -5)→U'(0, -4)


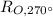
`R_(O,270^(\circ))` is a rotation 270° clockwise about the rotation. This negates the x-coordinate and switches it and the y-coordinate. Algebraically,
(x, y)→(y, -x)

When this is applied to R'S'T'U', we have:
R'(-2, -3)→R''(-3, 2)
S'(-1, -1)→S''(-1, 1)
T'(2, -1)→T''(-1, -2)
U'(0, -4)→U''(-4, 0)

These are the correct coordinates of R''S''T''U'', so this is the correct answer.

Answer 2

the correct answer is C on edge nuity