1. We have:

It's a
Piecewise-Defined Function, that is, a function defined by two or more equations over a specified domain is called a piecewise-defined function.

This is related to the
Greatest Integer Function (or
floor function).

This is related to the
Absolute Value Functiona) To find
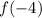
we choose the graph in which the function is defined for this value. As the line is defined for
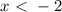
, then:
 b)
b) The function

has an absolute value function. This type of function is
absolutely positive except when it is zero. Therefore:
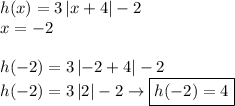
c) The parent function of the greatest integer function is shown in Figure 1. So:
![g(x)=[[x-1]]+2 \\ \\ x=2.4 \\ g(2.4)=[[2.4-1]]+2\\g(2.4)=[[1.4]]+2 \\ \\ From \ the \ figure: \\ \\ \boxed{g(2.4)=\mathbf{1}+2=3}](https://img.qammunity.org/2019/formulas/mathematics/high-school/u1ccsg8znm0pqlavv9v7yn680yfoj8c8su.png)
d) In
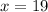 the function
the function
 is defined as:
is defined as:
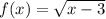
So:
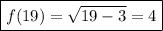
e) In this case:
![g(-0.9)=[[-0.9-1]]+2\\g(-0.9)=[[-1.9]]+2 \\ \\ From \ the \ figure: \\ \\ \boxed{g(-0.9)=\mathbf{-2}+2=0}](https://img.qammunity.org/2019/formulas/mathematics/high-school/pgglo9kn2lbc9uvyhn95hwu8lsmyphhrf5.png)
f) In this case:
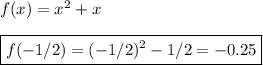
2. In this case we have a Piecewise-Defined Function too. So let's solve this problem.
a) We need to find the wage for the carpenter for four values. Therefore:
a.1) He works 30 hours, so we need to choose the function that is defined in this time, then:

a.2) The same function is valid because it includes
 , so:
, so:
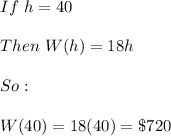
a.3) In this case he works 46 hours, so:
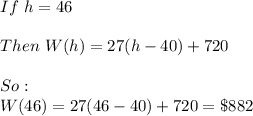
a.4) Here he is working 50 hours, so the same previous function is valid:
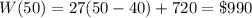
b) You can see the graph of this function in Figure 2. So let's explain what represents each term:
b.1) The representation of 27. This means that he earns time and a half for overtime. That is, if he works an hour (for less or equal than 40 hours) he earns $18 for each hour but from 41 hours and up he earns $9 further for each hour he works. In total he earns $27 for each hour ($18+9$) from 41 hours and up.
b.2) The representation of 720. This is the payment he gets for 40 hours worked. This term is always a constant value because when he works from 41 hours and up he obtaines this amount plus the extra money for the overtime.
b.3) The representation of
 . This term represents the overtime. That is, how many hours he works after 40 hours. So:
. This term represents the overtime. That is, how many hours he works after 40 hours. So:

c) They increased the regular work, so the new function is:
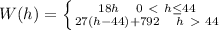
3. A new toy
a) The graph of this function is shown in Figure 3.
b) As you can see in the graph the vertex is the point:
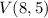
And this means the maximum sales the local store can get. The sales increase up to this point and they began to decrease.
c) We can get this by taking derivative, so:
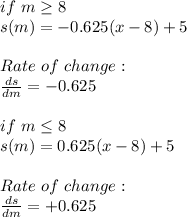
4. US Postal rates:
a) This is a step functions, that is, these are kind of functions whose graphs resemble sets of stairsteps. We can write it as follows:

b) According to the function this costs is $0.86, that is, we take the function in which
 is defined.
is defined.
5. Runner.
a) This is a Piecewise-Defined Function. This concept is stated above.
b) We can write this function as follows:

Therefore:
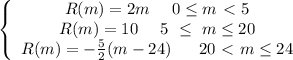
c) She increases it at the slope of the first line, that is:
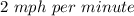
d.1)
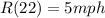
d.2) This represents her speed just in the minute 22.