Question

Find an equation for the plane containing the point (1, 1, 1) and the line (x, y, z) = (1 + 2t, 3 − t, t).

Answer 1

Explanation:

The line can be written as
`(x-1)/(2)= (y-3)/(-1)= (z-0)/(1) =t`

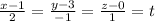
Since the line is contained in the plane, if we take any two points of this line they will lie in the plane.

Give values for t =0 and 1

We get two points (x,y,z) as (1,3,0) and (3,2,1)

Now we have another non collinearpoint (1,1,1) (given)

The plane equation can be written using these 3 points using the determinant.

x-x1 y-y1 z-z1

x2-x1 y2-y2 z2-z1

x3-x1 y3-y1 z3-z1 =0

Substitute the values form the points.

We get

`\left[\begin{array}{ccc}x-1&y-3&z-0\\2&-1&1\\0&-2&1\end{array}\right] =0`

Expand the determinant as

(x-1)(-1+2)-(y-3)(2-0)+z(-4-0) =0

x-1-2y+6-4z =0

x-2y-4z+5 =0