Question

Which rigid transformation would map ABC to ABF?

A) a rotation about point A
B) a reflection across the line containing CB
C) a reflection across the line containing BA
D) a rotation about point B

Answer 1

the answer is c. a reflection across the line containing ba

Answer 2

Answer: The correct option C. The figure shows the a reflection across the line containing BA.

Step-by-step explanation:

The rigid transforms means reflection, dilation and transformation.

In the given figure the two triangles are given ABC and ABF.

`CA=FA`

`\angle CAB=\angle FAB`

`AB=AB`

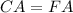
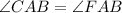
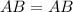
So by SAS the triangle CAB and FAB are congruent.

The common side is BA, so the figure shows the a reflection across the line containing BA. The point C and F are equal distance from the line BA. AS shown in below figure.

From the figure it is easily noticed that the triangle FAB is the mirror image of triangle CAB across the side AB.

Therefore the correct option is C.