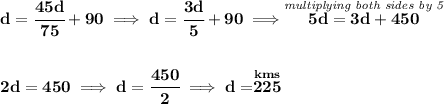Question

A train leaves a station and travels north at a speed of 45km/h. Two hours later a second train leaves on a parallel track and travels north at 75km/h. How far from the station will they meet ?

Answer 1

recall your d = rt, distance = rate * time.

A = first train.

B = second train leaving 2 hrs later.

if say by the time they meet, train B has traveled "t" hours, we know that train A has been traveling 2 hours more than that, because it left 2 hours earlier than train B, thus it has traveled "t + 2" hours.

keeping in mind that by the time they meet, they both have traveled "d" kilometers.


`\bf \begin{array}{lcccl} &\stackrel{km s}{distance}&\stackrel{km/h}{rate}&\stackrel{hours}{time}\\ &------&------&------\\ \textit{Train A}&d&75&t\\ \textit{Train B}&d&45&t+2 \end{array} \\\\\\ \begin{cases} d=75t\implies (d)/(75)=\boxed{t}\\\\ d=45(t+2)\\ ----------\\ d=45\left( \boxed{(d)/(75)}+2 \right) \end{cases}`


`\bf d=\cfrac{45d}{75}+90\implies d=\cfrac{3d}{5}+90\implies \stackrel{\textit{multiplying both sides by 5}}{5d=3d+450} \\\\\\ 2d=450\implies d=\cfrac{450}{2}\implies d=\stackrel{km s}{225}`