Question

What is the sum of the arithmetic sequence 8, 15, 22 …, if there are 26 terms?

2,483
2,485
3,487
3,489

Answer 1

Since the sequence is arithmetic, we have an expression of the form:

`an = a1 + d (n-1)`
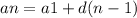
Where,
a1: first term of the sequence
d: common difference
n: number of terms
We look for the common difference:

`d = 22-15 = 15-8 = 7 d = 7`
Then, setting values we have:

`a26 = 8 + 7 * (26-1) a26 = 183`
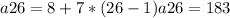
Then, the sum of the terms is:

`Sn = ((a1 + an) / (2)) * n`
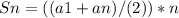
Substituting values:

`Sn = ((8 + 183) / (2)) * 26 Sn = 2483`
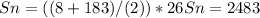Answer:
the sum of the arithmetic sequence 8, 15, 22 is:
Sn = 2483