Question

Write interval notation for the sets of x's described by the inequalities below:

a. X < 4
b. X ≥ 0
c. 0 < X ≤ 5
d. -2 ≤ X < 1
e. 0 < X < 1
f. -2 ≤ X ≤ 5

I don't understand what it's asking

Answer 1

Answers:
A:
`(-\infty, 4)`
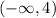
B:
`[0,\infty)`
C:
`(0,5]`
D:
`[-2,1)`
E:
`(0,1)`
F:
`[-2,5]`

=========================================

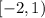
Explanations:

Interval notation is what the name implies: it describes an interval along a number line.

An interval is simply a region of the number line where you describe its starting point and ending point. If the interval goes off in one direction forever, then you use the infinity symbol (either plus or minus infinity depending on the direction)

-----------------------

Part A

We have an interval that doesn't have a left endpoint. It goes on forever in the negative direction. So the starting point is negative infinity. The ending point on the right is 4. We don't include 4 as part of the interval so we use a curved parenthesis instead of a square bracket.

That's why the answer to part A is
`(-\infty, 4)`

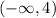
Note: always use a curved parenthesis with infinity. Why? Because we can't ever get to infinity (it's not a number, just a concept). We can only approach infinity.

-----------------------

Part B

Same idea as part A, but now we know the starting endpoint is x = 0. However, the right endpoint does not exist. The interval goes on forever to the right.

This is why the answer here is
`[0,\infty)`

The square bracket next to the 0 tells the reader "include 0 as part of the interval". Again, we exclude infinity from the interval as we never can reach infinity.

-----------------------

Part C

Unlike the first two parts, this part has a set beginning and set end. The left endpoint is 0, which we'll exclude. So we use a curved parenthesis here.

The right endpoint is 5, which is included. We use a square bracket here.

Put it all together and we get
`(0,5]` as the answer.
-----------------------

Part D

Same idea as part C. The key thing to notice is that we'll include the left endpoint while excluding the right endpoint. This is because of the "or equal to" portion of the inequality.

So we'll have a square bracket for the left endpoint -2
We'll have a curved parenthesis for the right endpoint 1

Answer:
`[-2,1)`

-----------------------

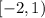
Part E

We will exclude both endpoints here. We'll use curved parenthesis for both endpoints.

The answer is
`(0,1)`
So x can be any number between 0 and 1; however x cannot equal 0, and x cannot equal 1 either.

Note: This looks identical to the ordered pair notation (x,y); however, we're not describing a point on the coordinate grid. We're still on the number line. Unfortunately there is no way around this confusing overlap.

-----------------------

Part F

This time we include both endpoints

The answer is
`[-2,5]` which says "x is some number in the interval from -2 to 5, including both endpoints"