Question

What is the sum of this geometric series? 16+24+...+81

Answer 1

The formula for a finite geometric series is:


`S_(n) = ( a_(1)(1-r^(n)) )/(1-r)`

a₁ is the first term of the geometric series. From the given series we can see that the first term of the series is 16.

r is the common ratio of the series. r can be found by dividing a term by its previous term. so r for the given series will be:

r = 24/16 = 3/2

n is the number of terms in the series. We can use the general formula of a Geometric Series to find the number of terms in the given series:


`a_(n) = a_(1) (r)^(n-1)`

We want to find at which number in the series is 81 located. Using the values, we get:


`81=16( (3)/(2) )^(n-1) \\ \\ \\ (81)/(16)= ((3)/(2))^(n-1) \\ \\ ( (3)/(2) )^(4) =((3)/(2))^(n-1) \\ \\ n=5`

This means, there are 5 terms in the given series.

Using the values in the formula, we get:


`S_(n)= (16(1-( (3)/(2) )^(5)) )/(1- (3)/(2) ) \\ \\ S_(n)=211`

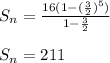This means, the sum of given geometric series is 211.