Question

Helppp me plzzz thank u thank u if u do

Answer 1

Try the 3rd one. But if you're not entirely sure, enter in each equation into a website called demos and see which one that matches

Answer 2

First, determine the slope of the line. See image attached.
The slope of the line could be determine using the formula:

`m = (\Delta y)/(\Delta x)`

`m = (-8)/(8)`
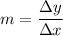
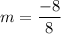
m = -1

Second, determine the equation of the line. The available information: m = -1 and one of the points that lies on the line is (x₁,y₁) = (0,-2).
Use this formula
y - y₁ = m(x - x₁)
y - (-2) = -1(x - 0)
y + 2 = -x
y + 2 = -x
x + y + 2 = 0

The answer is third option